In-Class

In-Class#

Coding Practice#

Code 8.1: Inventory Management#

Make a dictionary containing information about the inventory of a store where keys of the dictionary indicates the type of store item, for instance "apples", and its corresponding value corresponds to the quantity of that item in the store.

inventory = {
    "apples": 10,
    "bananas": 5,
    "oranges": 8,
    "kiwis": 7
}

Write a function restock_inventory that takes as input the dictionary inventory as well a restock amount.

The function should add the restock amount to each of items in the inventory and then return the updated dictionary.

The expected output of restock_inventory is shown below:

>>> inventory = {
...     "apples": 10,
...     "bananas": 5,
...     "oranges": 8,
...     "kiwis": 7
... }
>>> restock_inventory(inventory, 3)
{'apples': 13, 'bananas': 8, 'oranges': 11, 'kiwis': 10}
>>> restock_inventory(inventory, 2)
{'apples': 15, 'bananas': 10, 'oranges': 13, 'kiwis': 12}
>>> restock_inventory(inventory, 1)
{'apples': 16, 'bananas': 11, 'oranges': 14, 'kiwis': 13}

Code 8.2: Weather Station#

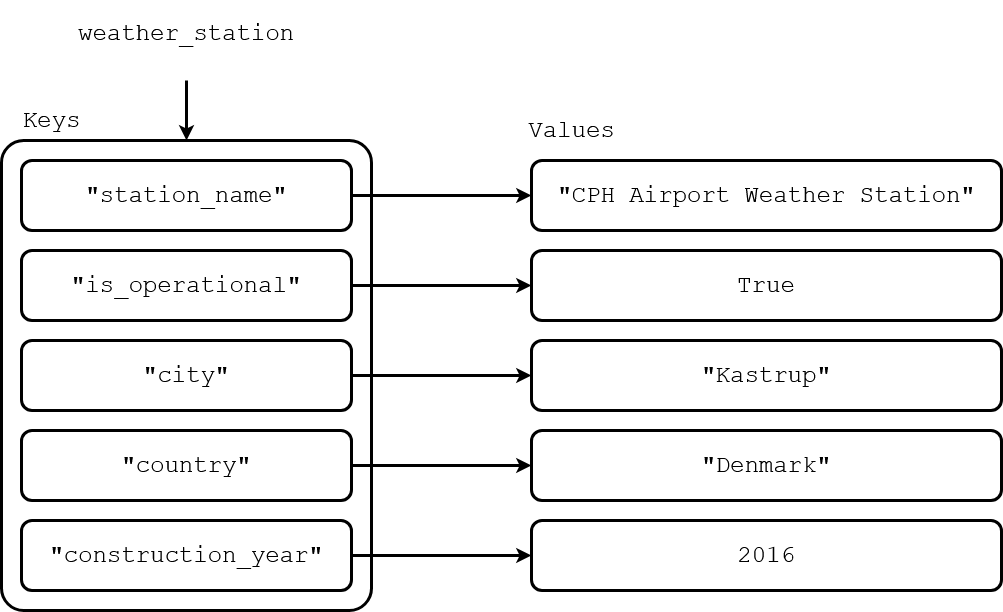
Define a dictionary which represents a weather station. The dictionary should have 5 keys: "station_name", "is_operational", "city", "country" and "construction_year". You can see in the image below, the value of each key.

Now you should modify the dictionary by adding the key temperature_readings with the value [20.1, 21.3, 19.8, 22.0]. Add also the key wind_speed_readings with the value [5.2, 3.4, 7.1, 15.6].

Write a for-loop that prints all key-value pairs of the dictionary weather_station. Look at your output and confirm that the dictionary has the correct keys and values.

Now write a function get_average_readings which as an input takes a dictionary with the same structure as weather_station. The function should return a tuple with two values: the average of the wind speed readings and the average of the temperature readings. Test the function with the dictionary weather_station and print the results.

Code 8.3: Data Statistics#

Write a function data_statistics which given a list of experiment values and an experiment name returns a dictionary containing the following key-value pairs:

experiment_name: The name of the experiment.
experiment_values: The list of experiment values.
mean_val: The mean of the experiment values.
standard_deviation: The standard deviation of the experiment values.
max_val: The maximum of the experiment values.
min_val: The minimum of the experiment values.

The standard deviation \(\sigma\) of a sequence of values can be found using the formula below:

\[ \sigma=\sqrt{\frac{\sum\left(x_i-\mu\right)^2}{N}} \]

where \(x_{i}\) denotes value \(i\) in the sequence, \(\mu\) is the mean of the sequence and \(N\) is the length of the sequence.

To test your function, you can use the example data given below:

experiment_name = "standard_values"
experiment_values = [1.30, -0.01,  1.35,  0.31,  0.35, -1.61,  1.39,  1.19, -1.07,  0.34]

Problem Solving#

Problem 8.X: Phonebook Merge (DEMO)#

A phonebook is represented as a dictionary where each key corresponds to a contact’s name, and the corresponding value is a list of phone numbers associated with that contact. As an example, consider the two phonebooks given below:

phonebook = {'Liv': ['55511112', '18777890'] ,
              'Mads': ['27274445', '48533336'],
              'Steve': ['45455555', '25455525']}

second_phonebook = {'Anna': ['89577772'] ,
                     'Steve': ['25257755', '25455525'],
                     'Mads': ['48533336', '27274445']}

Given a second phonebook, we want to add its content to the first phonebook, but without creating duplicates.

Write a function that takes two dictionaries representing phonebooks as input. The function should not have a return statement, but it should modify the first phonebook by adding the content from the second phonebook. Specifically:

If a name from the second phonebook is not present in the first phonebook, it should be added to the first phonebook along with its associated phone numbers.
If a name from the second phonebook is already present in the first phonebook, then we look at the two lists of phone numbers for that name. Phone numbers that are only present in the second list should be appended to the first list in the order they occur in the second list.

The function should have the following specifications:


            phonebook_merge.py

phonebook_merge(phonebook, second_phonebook)

Modifies the dictionary phonebook by adding the content from second_phonebook while avoiding duplicates.

Parameters:

`phonebook`	`dict`	A dictionary containing names and lists of phone numbers.
`second_phonebook`	`dict`	A second dictionary containing names and lists of phone numbers.

The expected behavior of phonebook_merge is shown below:

phonebook_merge(phonebook, second_phonebook)

for name in phonebook:
     name, phonebook[name]
     print(name, phonebook[name])

Liv ['55511112', '18777890']
Mads ['27274445', '48533336']
Steve ['45455555', '25455525', '25257755']
Anna ['89577772']

Problem 8.4: Energy Expenditure#

Energy expenditure is a measure of how many calories a body burns throughout a day. Total energy expenditure (TEE) can be calculated as

\[\mathrm{TEE} = \mathrm{BEE} \cdot \mathrm{AF}\]

where AF is the activity factor, and BEE is the basal energy expenditure covering essential functions like breathing, circulation, and digestion.

The BEE for males and females is

\[\mathrm{BEE}_\mathrm{male} = 66 + (13.7 \cdot \text{weight}) + (5.0 \cdot \text{height}) - (6.8 \cdot \text{age})\]

\[\mathrm{BEE}_\mathrm{female} = 655 + (9.6 \cdot \text{weight}) + (1.8 \cdot \text{height}) - (4.7 \cdot \text{age})\]

where weight, height and age are in kilograms, centimeters and years, respectively.

The activity factor AF is classified as:

Sedentary activity: \(\mathrm{AF} = 1.3\)
Moderate activity: \(\mathrm{AF} = 1.5\)
Strenuous activity: \(\mathrm{AF} = 2.0\)

Assume your are given data for three persons in the following form:

person_data = {
    "names": ["Jakob", "Josefine", "Morten"],
    "genders": ["Male", "Female", "Male"], 
    "ages": [25, 30, 37], 
    "weights": [70, 60, 86], 
    "heights": [175, 165, 189],
    "activity_levels": ["moderate", "strenuous", "sedentary"]
}

Here, the items in the first position of each list correspond to the weight, height and age of the first person, and so on.

Write a function calculate_bee_tee which meets the following specifications:


            calculate_bee_tee.py

calculate_bee_tee(person_data, name)

The basal energy expenditure (BEE) and total energy expenditure (TEE).

Parameters:

`person_data`	`dict`	Person data including age, gender, height and weight
`name`	`str`	The name of a person in `person_data`

Returns:

tuple

The BEE and TEE of the person with the corresponding name

The expected output of calculate_bee_tee is shown below:

>>> calculate_bee_tee(person_data, 'Jakob')
(1730.0, 2595.0)
>>> calculate_bee_tee(person_data, 'Josefine')
(1387.0, 2774.0)
>>> calculate_bee_tee(person_data, 'Morten')
(1937.6, 2518.88)

Problem 8.5: Player Scores#

You are in charge of making a leaderboard for DTU’s football club. You have devised a point scoring system to determine the performance of each player. The point scoring system is as follows:

Successful goals are worth 20 points each
Successful passes are worth 2 points each
Unsuccessful goal attempts are worth 5 points each
Unsuccessful pass attempts are worth 1 point each

The each player’s score is the sum of the points accumulated in the four categories.

Assume your are given the following set of player statistics containing number of goals, number of passes, number of goal attempts and number of pass attempts of all the players in the club. The attempts include both the successful and unsuccessful attempts.

player_stats = [
    {"name": "Bob", "goals": 2, "passes": 15, "goal_attempts": 3, "pass_attempts": 17},
    {"name": "Alex", "goals": 1, "passes": 17, "goal_attempts": 2, "pass_attempts": 20},
    {"name": "Molly", "goals": 1, "passes": 28, "goal_attempts": 2, "pass_attempts": 31},
    {"name": "Sophia", "goals": 2, "passes": 21, "goal_attempts": 3, "pass_attempts": 25}
]

Write a function get_highscore which meets the following specifications:


            get_highscore.py

get_highscore(player_stats)

Finds the player with the highest score from a set of player statistics.

Parameters:

player_stats

list

A set of player statistics including player name, number of goals, number of passes, number of goal attempts and number of pass attempts.

Returns:

tuple

The name of the highest scoring player and their player score.

The expected output of get_highscore is shown below:

>>> get_highscore(player_stats)
('Sophia', 91)

Problem 8.X: Booklet layout (ET)#

A booklet may be made by folding sheets of paper, as in the illustration below. When only one sheet of paper is used, the booklet has 4 pages. If two sheets are used, the booklet has 8 pages. Every additional sheet contributes with 4 pages. Therefore, the number of pages in a booklet is always a multiple of 4.

If we have a certain number of pages with content, and this number is not a multiple of 4, there will be up to 3 blank pages at the end of the booklet.

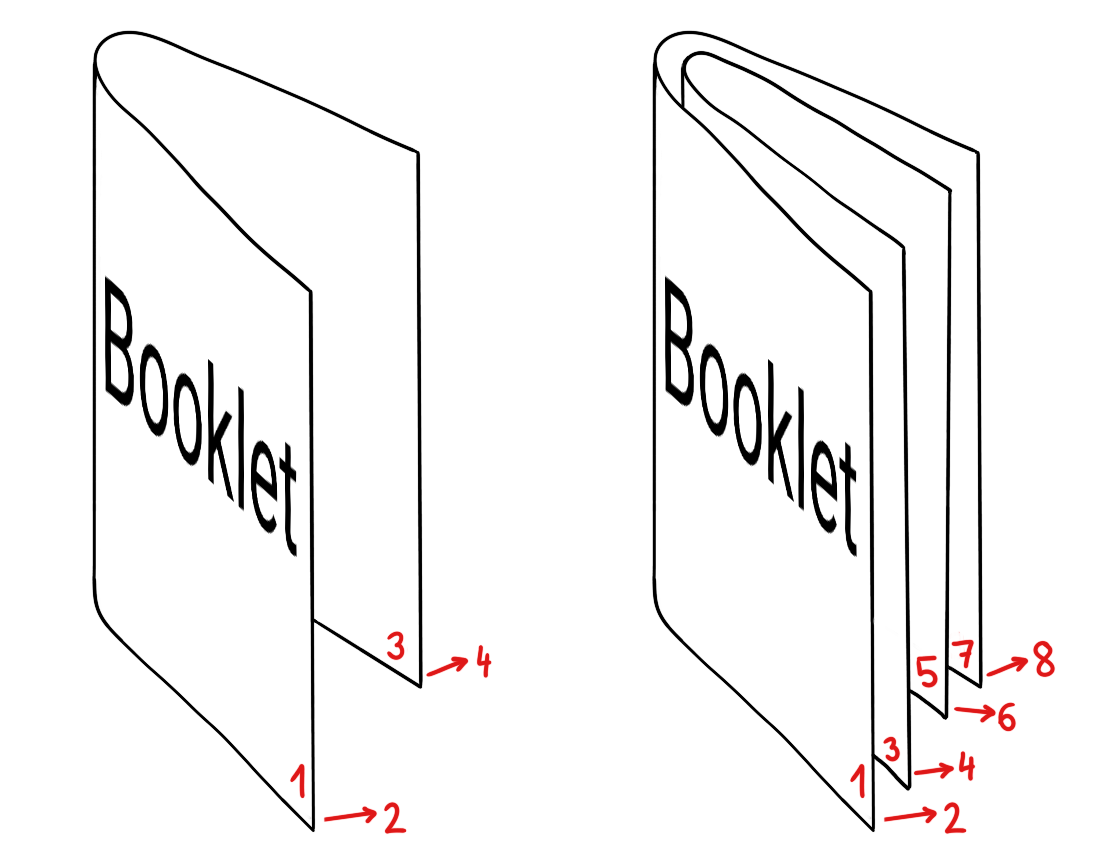
Given a number of pages with content to be placed in a booklet, we want to know two things:

the total number of pages in the smallest booklet that can accommodate the content,
the number of blank pages in such a booklet.

Write a function that takes as input the number of pages of content. The function should return the total number of pages in the smallest appropriate booklet, and the number of blank pages.

As an example, consider having 17 pages with content. Number 17 is not a multiple of 4, so pages need to be added. Adding one or two blank pages will not be enough, since neither 18 nor 19 are multiples of 4. Adding three blank pages will give 20, which is a multiple of 4. Therefore, the booklet has 20 pages, and there will be 3 blank pages. The desired output is shown in the code cell below.

>>> booklet_layout(17)
(20, 3)

The filename and requirements are in the box below:


            booklet_layout.py

booklet_layout(content_pages)

Return the number of total and blank pages given content.

Parameters:

content_pages

int

A positive integer, the number of pages with content.

Returns:

tuple

The number of total pages and the number of blank pages.

Problem 8.X: Name frequency (ET)#

Given a list of full names, we need to know how many times each first name occurs in the list. Here, the first name is the part of the full name before the first space.

Write a function that takes a list of full names as input. The function should return a dictionary where the keys are the first names from the list. The value of each key should be the number of times this first name occurs in the list.

As an example, consider the input below.

>>> names = ['Liv Ea Jensen', 
...         'Mads Oliver', 
...         'Steve Madsen',
...         'Anna Simon', 
...         'Simon Gade', 
...         'Mads Kai Jensen']

The first names are Liv, Mads, Steve, Anna, Simon, and Mads. The first name Mads occurs twice, and the other first names occur once. The function should therefore return the dictionary with keys and values as shown below.

>>> my_name_frequency = name_frequency(names)
>>> for name in my_name_frequency:
...     print(name, my_name_frequency[name])
Liv 1
Mads 2
Steve 1
Anna 1
Simon 1

The filename and requirements are in the box below:


            name_frequency.py

name_frequency(names)

Return frequency of names in the list.

Parameters:

names

list

A list of strings.

Returns:

dict

The frequency of names.

`social_network`	`dict`	A social network model.
`person_name`	`str`	The name of a person in `social_network`.

In-Class

Contents

In-Class#

Coding Practice#

Code 8.1: Inventory Management#

Code 8.2: Weather Station#

Code 8.3: Data Statistics#

Problem Solving#

Problem 8.X: Phonebook Merge (DEMO)#

Problem 8.4: Energy Expenditure#

Problem 8.5: Player Scores#

Problem 8.6: Social Network#

Problem 8.X: Booklet layout (ET)#

Problem 8.X: Name frequency (ET)#